Regresní a korelační analýza

Korelace

Tento pojem pochází původně z latiny a znamená vzájemný vztah mezi dvěma veličinami (v našem případě to mohou být procesy). Vztah je popisován, tak že pokud nastane změna u jedné veličiny, tak se pak změna musí projevit i u druhé, jelikož obě na sobě závisejí.  Avšak korelace ještě neznamená kauzalitu, tedy příčinnost (vztah mezi příčinou a následkem) více

Mírou nebo ukazatelem korelace mezi dvěma spojitými veličinami je koeficient r. Koeficient nabývá hodnot v intervalu [-1;1], kdy hodnota r= -1 mě informuje o dokonalém záporném lineárním vztahu, hodnota r=0 mě informuje o neexistenci lineárního vztahu a hodnota r=1 indikuje dokonale čistý lineární vztah. Tato metoda bývá používána ve fázi Analyze.

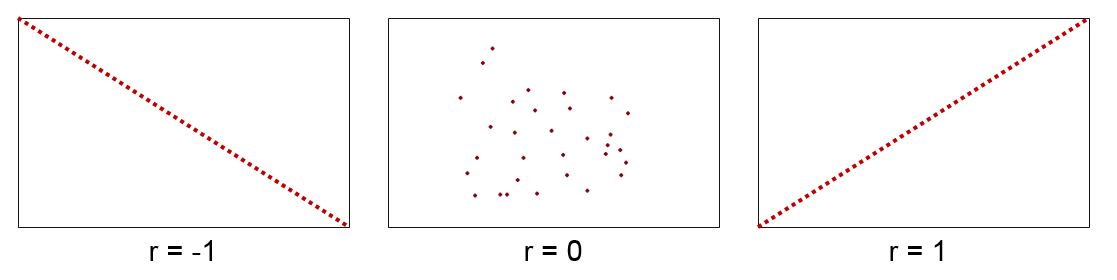
Korelačních vztah lze vyjádřit graficky, ale grafická podoba musí být ještě otestována, abychom zjistili významnost hodnoty r. Testuje se pomocí hypotézy a hodnoty P-Value. Pokud je P-Value < 0.5, tak korelační koeficient statisticky významný a mezi zkoumanými veličinami existuje lineární vztah.

Na příkladu si ověříme jestli existuje lineární vztah mezi počtem prodejů jednotlivých prodejců..více

Regresní analýza

Regresní analýzou zjišťujeme závislost našeho vstupu (X₁,X₂….) na výstupu (Y).  Cílem regresní analýzy je odhadnout tento vztah co nejpřesněji. Oproti korelační analýze nehledáme pouze lineární vztah. Tedy naměřenými daty se proloží křivka, aby co nejlépe vystihla chování vzorku naměřených dat. V ideálním a nejjednodušším případě se bude jednat o lineární vztah, lineární regresi.

Při výběru správné regresní funkce se používá metoda nejmenších čtverců, tedy hledáme funkci, která leží nejblíže hodnotám našeho vzorku dat. Funkce, jak už bylo zmíněno nemusí být pouze lineární, ale třeba kvadratická, kubická či logaritmická. Ukazatelem správnosti modelu je tzv. koeficient determinace R².

• Koeficient determinace R² – ukazatel adekvátnosti modelu, tu vyjadřuje v procentních bodech a říká nám kolik procent variability výstupu (Y) je způsobeno našimi vstupy (X₁,X₂….) či vstupem.
• Koeficient determinace upravený R² (adj) – upravený koeficient determinace, který zohledňuje počet prediktorů v modelu. více

Pro analýzu musí být splněny předpoklady normálního rozdělení a nezávislosti reziduí. V Minitabu nalezneme pod následující cestou.

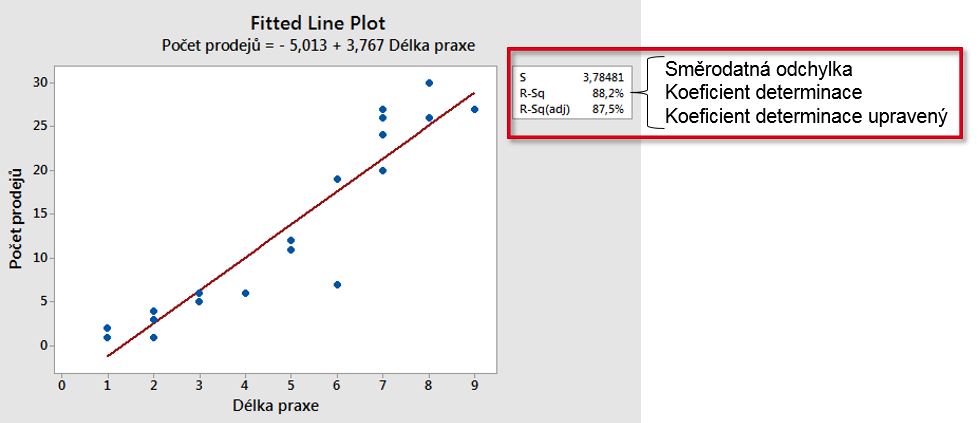
V plovoucím okně po zadání vstupů a výstupů je nezbytné zadat i typ očekávaného regresního modelu. V prvním případě jsme vybrali model lineární, kdy R² je 88.2% a regresní rovnice, která popisuje naši závislost délky praxe na počtu prodejů je Počet prodejů = -5.013 + 3.767 * Délka praxe.

Při volbě kvadratického modelu, zjistíme, že pro náš příklad je tento model o něco vypovídavější více

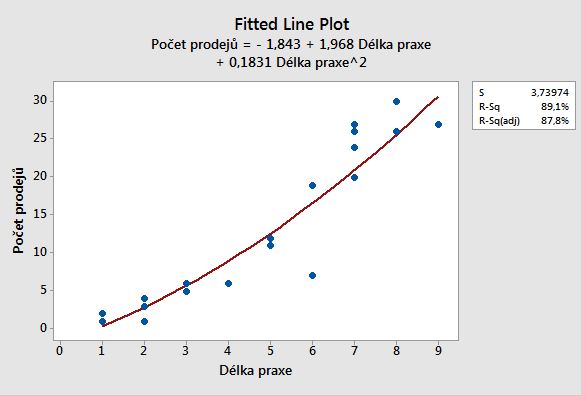
Při volbě kvadratického modelu, zjistíme, že pro náš příklad je tento model opět o něco vypovídavější, kdy R² se rovná více