Spojitá data

ANOVA

Jde o zkratku anglických slov ANalysis Of VAriance – tedy ANOVA.  ANOVOu se porovnávají aritmetické průměry vybraných skupin. Pomocí této analýzy můžeme ověřit, zda pozorované veličiny se od sebe statisticky liší. Tedy, porovnávají se vzájemné polohy dat pozorovaných skupin. Podmínkou pro použití ANOVY je normalita dat. Normalitu mohu ověřit pomocí testu normality více 

K čemu můžeme ANOVU použít?

Poměrně snadno můžeme získat odpovědi na otázky typu:

• Trvá obsluha klienta na všech pobočkách stejně dlouho?
• více

Příklad:

Chceme porovnat jestli je rozdíl ve zpoždění vlaků přijíždějících z různých směrů. Máme celkem čtyři směry a v každém jsme měřili týden. Předpokládáme, že data jsou normální. Avšak je vždy nutné data ověřit testem normality. V Minitabu si najdeme následující cestu:

V rolovacím okně vybereme Response data are in a separate…., jelikož data máme v různých datových sloupcích. Sloupce vybereme s kolonce Responses. V podmenu Graphs si můžeme vybrat, jaké grafy chceme zobrazit. A dáme OK.

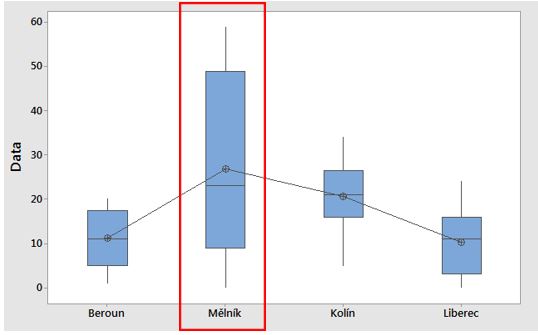
Zajímají nás poloha dat (mediány, průměry atd.), proto volím graf boxplot. Na první pohled je zřejmé, že se datové vzorky liší. Zejména data naměřená u vlaku ze směru Mělník.

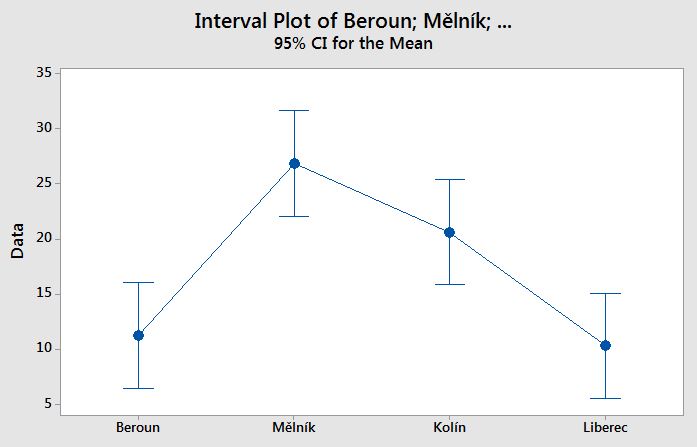
Interval plotem porovnáme kolísání, jak uvnitř, tak i mimo skupiny. V tomto případě je kolísání uvnitř skupin shodné na rozdíl od kolísání vně skupin. Tedy můžeme zamítnout nulovou hypotézu.

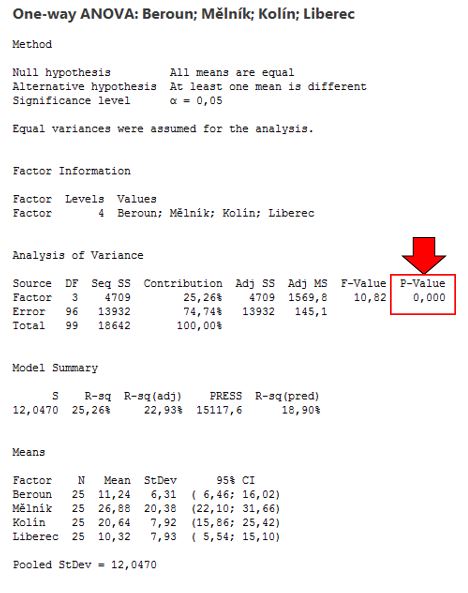
Ještě je dobré si situaci potvrdit výpisem z analýzy, kdy nás hlavně zajímá hodnota P-Value, která je v tomto případě rovna 0. To znamená, že zamítám nulovou hypotézu, že všechny průměry jsou stejné a přijímám alternativní. Minimálně jeden průměr se statisticky liší.

Test Normality

Zda jsou data normální či nikoliv, mohu velice snadno ověřit pomocí testu normality. Cestu k němu naleznete na obrázku níže. Poté v plovoucím okně stačí jen vybrat datový sloupec, který chcete testovat a dát ok.

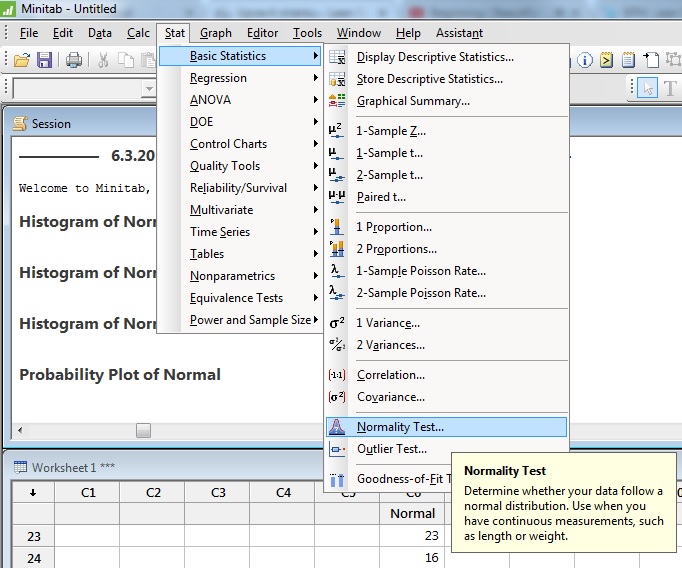
Následně se vám objeví graf podobný tomu na obrázku dole. Nejdůležitějším údajem v legendě grafu je P-Value, která mi odpovídá na otázku: Jsou data normální?

• Hodnota P-Value > 0.05, tak s největší pravděpodobností více 
• Hodnota P-Value < 0.05 více 

Kruskal – Wallis Test

Tento test je používaný k porovnání dvou a více nezávislých vzorků dat stejných nebo různých velikostí. Je to neparametrická metoda, tudíž není vyžadována normalita dat. Porovnáváme vzájemnou polohu dat. Kruskal – Wallis je obdobou ANOVY, avšak pro neprarametrická rozdělení, proto platí i formulace výše uvedených otázek pro které je možno získat testem odpovědi. Na rozdíl od ANOVY neporovnává aritmetické průměry skupin, ale mediány. Tedy jedná se slabší test než je ANOVA, jelikož je zde vyšší pravděpodobnost chybného rozhodnutí na základě analýzy.

Příklad:

Chceme porovnat jestli je rozdíl ve zpoždění vlaků přijíždějících z různých směrů. Máme celkem čtyři směry a v každém jsme měřili týden. Avšak je vždy nutné data ověřit testem normality. V Minitabu si najdeme následující cestu:

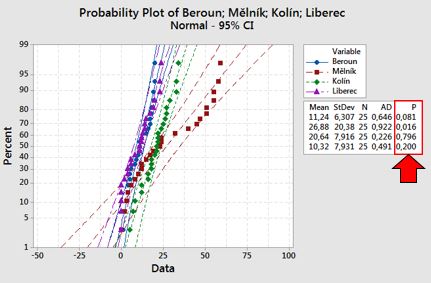
Z výsledků vyplývá, že druhá skupina má P-Value pouze 0.016 a tedy nemá více

Test rovnosti rozptylů

Neboli test for equal variances, tímto testem porovnáváme kolísání dat mezi dvěma nebo více vzorky dat. Tento test se používá v případě, že potřebujeme porovnat rozptyly skupin dat a to zejména pokud mají stejnou polohu. Poloha je dána většinou průměrem, ten může být v toleranci, avšak jednotlivá měření již být nemusí a v souboru dat může být větší množství případů, kdy byly naměřeny hodnoty mimo hranice procesu.

Příklad:

Chceme porovnat jestli je rozdíl v kolísání ve zpoždění vlaků přijíždějících z různých směrů. Máme celkem čtyři směry a v každém jsme měřili týden. Avšak je vždy nutné data ověřit testem normality. V Minitabu si najdeme následující cestu:

Z výsledků vyplývá, že druhá skupina má P-Value pouze 0.016 a tedy více . Nachází-li se v souboru skupin, alespoň jedna, která nemá normální rozdělení, sledujeme Levene’s Test, jinak Barlettův test (Multiple Comparison). Test rovnosti rozptylů nalezneme v Minitabu pod následující cestou:

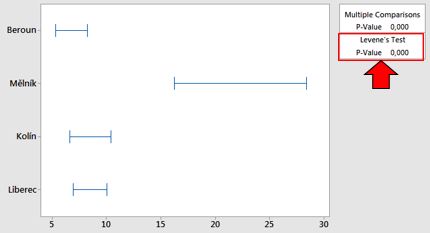
P-value je menší než 0.05 a tedy více. Rozptyly nejsou homogenní.

Diskrétní data

Chí – kvadrát

Někdy můžete také tento test nalézt pod názvem test dobré shody. Test se používá při porovnávání podílů počtů např. produktů, prodejů, defektů, zmetků, podíly investic, chyb na produktu nebo na formuláři.

• Nulová hypotéza H₀ je vždy : Podíly se sobě ve skupinách rovnají
• Alternativní hypotéza H₁: Podíl alespoň jedné ze skupin je statisticky odlišný od podílu některé jiné skupiny

Příklad:

Máme čtyři prodejce a chceme si porovnat jejich výkony a případně ověřit, zda nepracují pod své možností. Máme k dispozici data za poslední rok, která udávají kolik prodejce uzavřel obchodů a kolik obchodů zůstalo pouze příležitostmi. Data vypadají následovně:

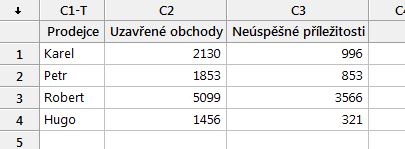
Test nalezneme pomocí cesty: